Abstract
Sparse activation, which selectively activates only an input-dependent set of neurons in inference, is a useful technique to reduce the computing cost of Large Language Models (LLMs) without retraining or adaptation efforts. However, whether it can be applied to the recently emerging Small Language Models (SLMs) remains questionable, because SLMs are generally less over-parameterized than LLMs. In this paper, we aim to achieve sparse activation in SLMs. We first show that the existing sparse activation schemes in LLMs that build on neurons’ output magnitudes cannot be applied to SLMs, and activating neurons based on their attribution scores is a better alternative. Further, we demonstrated and quantified the large errors of existing attribution metrics when being used for sparse activation, due to the interdependency among attribution scores of neurons across different layers. Based on these observations, we proposed a new attribution metric that can provably correct such errors and achieve precise sparse activation. Experiments over multiple popular SLMs and datasets show that our approach can achieve 80% sparsification ratio with <5% model accuracy loss, comparable to the sparse activation achieved in LLMs.
Sparse Activation Difference between LLMs and SLMs
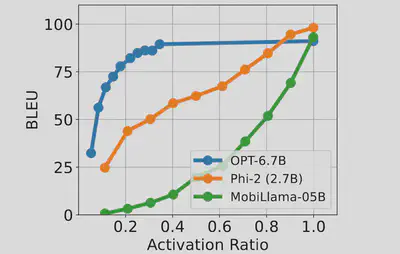
As shown in the Figure, OPT-6.7B is highly over-parameterized such that we only need to activate <40% of neurons to achieve the maximum accuracy. In contrast, MobiLlama-0.5B and Phi-2 are much less over-parameterized, and both require almost all neurons to be activated to avoid accuracy loss. Even when a small percentage of neurons with the smallest magnitudes are deactivated, the model accuracy significantly drops. These results show that for SLMs, neurons’ output magnitudes cannot precisely measure the neurons’ importance in inference, and hence cannot be used as the metric for sparse activation.
Using Attribution Scores as Neuron Importance
A better approach is to measure neurons’ importance in inference with their attribution scores, and further use such attribution scores for sparse activation. In general, attribution methods quantify the correlation between input data, intermediate features and model output, and most recent methods calculate neurons’ attribution scores from their gradients and outputs. We investigated the effectiveness of representative gradient-based attribution metrics, as listed below, when evaluating a neuron’s importance for sparse activation.
- Gradient × Output (GxO): It calculates the first-order approximation of the change of model output when the neuron is deactivated, as $\partial F(x) / \partial x \cdot x$, where $x$ is the neurons’ output scalar and $F$ is a function that maps neoron’s output to the model output.
- SNIP: It considers only the sensitivity of neuron’s output change on the model output as $| \partial F(x) / \partial x \cdot x|$.
- Fisher information: It calculates the square value of SNIP, and hence ranks the importances of different neurons in the same ways as SNIP does.
- Integrated Gradients (IG): It calculates the neuron’s contribution to the change of model output by interpolating between x and a baseline (usually zero output) and averaging the gradients at these interpolations.
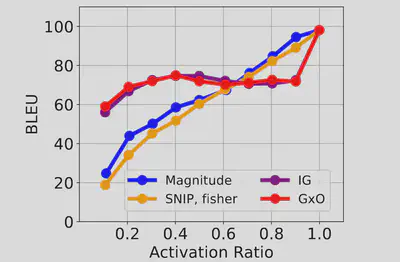
As shown in the Figure below, IG and GxO achieve the highest and very similar levels of model accuracy. Due to IG being computationally expensive, GxO’s first-order approximation to attribution is a better choice.
Attribution Errors due to Interdependency
As shown in the Figure below on the left, whenever some neurons are deactivated, such deactivation changes the attribution scores of other activated neurons, both in the same layer and in other subsequent layers. These changes, in many cases, could also change the rankings of neurons’ attribution scores and hence result in suboptimal selection of neurons being deactivated, given a required activation ratio.
Results in Figure below on the right show that such impact significantly grows with higher activation ratios. The basic reason is that when the activation ratio is high, only few neurons are deactivated. We also found that attribution errors produce much higher impacts on MLP neurons, because the number of MLP neurons is usually much larger than the number of attention heads, and the rank of MLP neurons’ attention scores is hence easier to be changed.
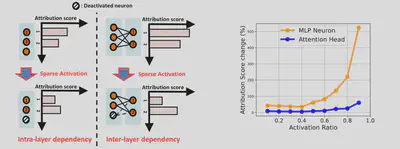
We are then motivated to develop techniques that can effectively mitigate these attribution errors and optimize the accuracy-sparsity tradeoffs in SLMs with proper sparse activation. In particular, the intra-layer dependency only reflects changes in the current layer’s gradients because the outputs of neurons in the same layer are independent from each other. In contrast, the inter-layer dependency reflects changes in both the neuron outputs and gradients of the subsequent layer, as they all depend on the outputs of the previous layer. Hence, we mainly focus on mitigating the errors caused by inter-layer dependency.
Attribution Error Correction
Our approach is to first analyze and quantify the attribution error caused by inter-layer dependency, and then mitigate such error by adding a corrective term onto each neuron’s attribution calculated with the GxO metric, so that we can ensure proper sparse activation by calculating all neurons’ attributions in one shot. More specifically, we formally proved the lower and upper bounds of the attribution error, and further provided practical methods of calculating and applying such corrective terms based on these bounds.
Our Proposed Corrective Term
Without loss of generality, we use a case of two layers in a SLM, namely $L_1$ and $L_2$, to quantify the attribution error caused by inter-layer dependency. $L_2$ is a deeper layer than $L_1$. $L_1$’s neuron output $\textbf{X} = (x_{1}, x_{2}, \ldots{}, x_{N_1})$. We use $F( \cdot )$ to represent the function that maps the output of $L_1$ to the model output.
With a reasonable assumption that intra-layer dependency has minimal impact on attribution error, we can assume that applying masking does not change the neuron gradients in the same $L_1$ layer. In this scenario, we could prove the Theorem that the error of inter-layer dependency caused by deactivating neuron $i$ in $L_1$ has a lower bound of $0$, and an upper bound of $| x_i | \cdot \sqrt{ \sum_{k=1}^{N_1} { ( \frac{\partial F}{\partial x_k } ) }^{2} } $, where $x_k$ is the output of another neuron $k$ in $L_1$. The proof can be found in Section 3.2 of our paper.
On top of the Theorem above, we experimentally show that the distribution of attribution errors follows a truncated normal distribution with a high confidence interval. As a result, we calculate the corrective term as $$ C(i) = \frac{1}{2} \cdot | x_i | \cdot \sqrt{ \sum_{k=1}^{N_1} { ( \frac{\partial F}{\partial x_k } ) }^{2} } $$
This corrective term is only related to the output magnitudes and gradients of neurons, and hence such corrective terms of all neurons can be computed in one shot with vectorized computations enabled in the existing deep learning APIs.
In the actual computation, the corrective term is added onto the attribution score of neuron $i$ in $L_1$ calculated without deactivation, which is denoted as $S(F, x_{i})$ in the paper. In our experiments, we use GxO’s first-order approximation to compute $S( \cdot )$.
Main Results
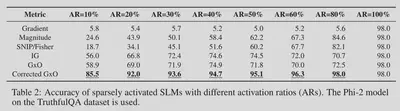
We evaluate the model accuracy with different activation ratios (ARs), using the Phi-2 model on the TruthfulQA dataset. Results in the Table below show that, when applying our proposed corrective term onto the GxO metric, our approach generally achieves much higher model accuracy than all baselines.